Nuevos modelos del problema del castor afanoso pueden conducir a un nuevo paradigma de computación

Ya hemos hablado con anterioridad acerca del castor afanoso y de su equivalencia con el problema de la parada que -recordemos- es el ejemplo paradigmático de problema no computable y sobre el que se asienta toda una jerarquía de clases de problemas basadas en oráculos para la resolución del mismo. El problema del castor afanoso enraiza pues de forma esencial en el modelo de computación de Turing, por lo que resulta fundamental avanzar en su compresión y resolución. Precisamente en este sentido hay que enmarcar un reciente trabajo de H.R. Peinetti y colaboradores -de la Universidad Nacional de La Pampa, la Colorado State University y el U.S. Geological Survey- titulado

• Simulation modeling to understand how selective foraging by beaver can drive the structure and function of a willow community

y publicado en Ecological Modelling. En este trabajo Peinetti et al. presentan un modelo de las complejas interacciones del castor con su entorno y con su comunidad. Los resultados de simulaciones a largo plazo del modelo arrojan revelaciones de gran interés en relación con el comportamiento asintótico del castor afanoso, lo que a su vez constituye una información de enorme valor con vistas a la construcción de oráculos para el mismo. De llegar a sustanciarse estos oráculos estaríamos en puertas de un salto trascendente en los modelos de cómputo vigentes, lo que sugiere que quizás otras líneas actuales de investigación en computación cuántica o computación con ADN deberían irse paulatinamente redireccionando hacia el área del artículo reseñado.

Actualización: Como el lector habrá advertido con toda seguridad, este artículo es sólo una broma, cumpliendo con la tradición del 28 de diciembre. Por más que la vida social del castor pueda ser apasionante, los investigadores en computación cuántica pueden estar tranquilos: no es previsible que tengan que dedicarse a estudiar estados de superposición de estos simpáticos roedores.

Conocimiento Peligroso: Cantor, Boltzmann, Gödel, Turing

«Conocimiento Peligroso» («Dangerous Knowledge«) es el título de un documental de la BBC sobre cuatro grandes genios de las matemáticas cuya salud mental se deterioró durante el curso de su carrera científica, y que acabaron suicidándose: Georg Cantor, Ludwig Boltzmann, Kurt Gödel y Alan Turing.

La hipótesis subyacente en el documental es que de alguna manera fue la extrema brillantez de estos matemáticos la que les causó en última instancia la locura y el suicidio, debido a una progresiva inmersión en el mundo matemático que estudiaban, y a la interiorización de las implicaciones filosóficas de los resultados que obtuvieron. Se trata de una hipótesis un tanto simplista ya que no tiene en cuenta las azarosas circunstancias personales que rodearon la vida de cada uno de ellos, aunque ciertamente es posible que la forma en la que se volcaron hacia la investigación matemática jugara también su papel para el desenlace final. Es en cualquier caso una buena excusa para ver retazos biográficos de estas cuatro figuras de la ciencia.

El documental está disponible en YouTube organizado en 11 fragmentos, cada uno de entre 5-8 minutos de duración:

• El Mensajero de Dios: Georg Cantor (1, 2, 3)
• El Genio del Desorden: Ludwig Boltzmann (4, 5, 6)
• Los Límites de la Lógica: Kurt Gödel (7, 8)
• El Enigma: Alan Turing (9, 10, 11)

Un aspecto interesante del documental son los comentarios de algunos científicos relacionados con el tema, como Roger Penrose y Gregory Chaitin. Es divulgativo y poco profundo, pero entretenido de ver de rato en rato.

Un conjunto de Mandelbrot del tamaño del Universo visible

Zambullirse en un fractal es siempre una experiencia interesante. El vídeo de abajo muestra una de estas zambullidas en el conjunto de Mandelbrot, profundizando de tal manera que si la escena final se asume de un tamaño similar al del monitor, la escena inicial tendría un tamaño superior al del Universo visible. Esto quiere decir que la magnificación es de unos 27 órdenes de magnitud.

Hay que recordar que el conjunto de Mandelbrot es el conjunto de los puntos c del plano complejo tales que la sucesión {0, f(0), f(f(0)), …, fⁿ(0), …} está acotada cuando n tiende a infinito, siendo f(z) = z² + c. El resultado es un conjunto conexo con una enorme riqueza morfológica en la zona de transición entre los puntos que pertenecen al conjunto y los que no. Se sabe que si para un cierto valor de c algún miembro de la sucesión tiene módulo mayor que 2, entonces c no pertenece al conjunto. Esto quiere decir que el complementario del conjunto de Mandelbrot es recursivamente enumerable (si asumimos que c es un número complejo expresable mediante números racionales). La cuestión de si el propio conjunto de Mandelbrot es recursivamente enumerable está aún abierta.

No por conocida es menos impactante la complejidad de las estructuras que nos vamos encontrando a medida que descendemos al sub-universo de Mandelbrot, con componentes auto-similares de diferente aridad. Es un viaje que sin duda no desmerece al que realizó David Bowman.

Turing en una cáscara de nuez: Complejidad de Kolmogorov

Aprovechando unos minutos de inusual relax para la época del año en la que nos encontramos, vamos a continuar la serie sobre computabilidad. En el último apunte al respecto vimos el problema del castor afanoso que -entre otras cosas- es especialmente interesante porque proporciona un primer nexo entre calculabilidad y complejidad descriptiva. Hay que recordar que la función castor afanoso se define como el mayor valor generable por un programa de cierta longitud, y que tal como vimos no es computable. Vamos ver hoy una noción más general y realmente interesante: la complejidad de Kolmogorov.

Imaginemos que tenemos una secuencia s de símbolos tomados de un cierto alfabeto Σ. Por simplicidad, y sin pérdida de generalidad, vamos a suponer que Σ={0,1}, y que por lo tanto estamos hablando de cadenas binarias. Supongamos ahora que queremos describir esta secuencia, donde por describir nos referimos a proporcionar información suficiente para poder reproducir dicha secuencia. Informalmente hablando, si la secuencia es simple, la cantidad de información necesaria para esta descripción será pequeña (por ejemplo, una cadena formada exclusivamente por ceros puede ser descrita simplemente dando su longitud, y aclarando que todos los símbolos son ceros). Por otra parte, es posible que no seamos capaces de discernir ningún patrón en los símbolos, y no nos quede otro remedio que usar la misma secuencia como su propia descripción.

De una manera más formal, imaginemos un cierto lenguaje L que usaremos para describir las cadenas de símbolos. Puesto que queremos evitar la ambigüedad del lenguaje natural, vamos a emplear un lenguaje puramente computacional. Por ejemplo, podemos considerar que L es nuestro lenguaje de programación favorito: haskell, perl, smalltalk, … Entonces, una descripción de una cadena de símbolos será un programa que la genera, e.g., la imprime en pantalla. Hecho esto, definimos la complejidad de Kolmogorov K(s) de una cierta cadena de símbolos s como el tamaño (definido de alguna manera razonable) del programa más pequeño que la genera.

Una primera consideración que nos puede venir a la mente de manera inmediata es que dicho tamaño es muy dependiente del lenguaje descriptivo que empleemos. La dependencia es cierta, pero no es muy preocupante ya que se reduce a una cierta constante, esto es, dados dos lenguajes L₁ y L₂, y cualquier cadena de símbolos s, |K₂(s)-K₂(s)| < c. Esto puede parecer sorprendente, pero no lo es, ya que lo único que necesitamos para pasar de una descripción en L₁ a otra en L₂ es un programa intérprete de L₁ escrito en L₂. Dicho intérprete podrá ser más o menos largo, pero es fijo, por lo que su tamaño es una constante (y el tamaño del programa correspondiente en L₂ es el tamaño del programa en L₁ más el del intérprete). Otro resultado interesante pero menos sorprendente es que existe una constante c (dependiente del lenguaje) tal que para cualquier cadena s, K(s) < |s| + c. Esto es fácil de ver, si pensamos que en el peor caso basta con confeccionar un programa que contenga la propia cadena como constante interna.

Dicho lo anterior, uno de los aspectos más interesantes de la complejidad de Kolmogorov es el que hace referencia a la noción de compresibilidad. Si tenemos una cadena s y un programa P más pequeño que s que la describe, entonces dicho programa puede interpretarse como una compresión (sin pérdida de información) de s. Por lo tanto, si K(s)<|s| diremos que s es compresible. Es fácil ver que no todas las cadenas son compresibles, esto es, hay cadenas s que son incompresibles: K(s) >= |s|. Por ejemplo, si P es el programa más pequeño que describe a s (i.e., K(s) = |P|), y pudiéramos comprimir al propio P usando el mismo lenguaje en el que está escrito, tendríamos una descripción Q más corta de s, lo que suponíamos que no existía. Siendo estrictos, en realidad una vez que ejecutáramos Q, tendríamos que dar la orden de ejecutar la salida que ha producido –P– para obtener s, por lo que incluyendo el tamaño de dicha orden llegamos a que K(s) >= |s|-c (y decimos entonces que s es c-incompresible). En cualquier caso, existen (|Σ|ⁿ-1)/(|Σ|-1) cadenas de menos de n símbolos, y |Σ|ⁿ cadenas de n símbolos, esto es, más que la primera cantidad por lo que no se puede hacer una correspondencia biyectiva entre ellas, y por lo tanto existen cadenas 1-incompresibles.

El próximo día exploraremos más en detalle las propiedades algorítmicas de la complejidad de Kolmogorov, y veremos que no sólo no es computable, sino que a través de ella llegamos una vez más a los teoremas de incompletitud de Gödel.

Caos, no linealidad, y espontaneidad en el comportamiento de los insectos

«La aleatoriedad es sólo una medida de nuestra ignorancia sobre
las causas que provocan un determinado evento.»

Pierre Simon Laplace (1749-1827), matemático francés

Hace unos días Pjorge recuperaba una reseña sobre un libro de John Searle en el se que abordaba el tema de la consciencia humana. A raíz de esta reseña, hubo un interesante mini-debate en el hilo de comentarios sobre si la consciencia humana era una propiedad
algorítmica o no, y elaborando sobre este tema, una de las consideraciones que surgió hacía referencia a la posibilidad de que organismos anteriores a los humanos en la cadena evolutiva tuvieran un comportamiento modelable algorítmicamente. Es algo que parece razonable (al menos me lo pareció en primera instancia), pero que puede que no sea tan trivial de asumir. Precisamente, a través de MarkCC he llegado a un artículo que analiza cuestiones muy relacionadas con las anteriores consideraciones. Se trata concretamente de un trabajo de Alexander Maye y colaboradores, titulado

• Order in Spontaneous Behavior

que acaba de ser publicado hace un par de días en PLoS ONE (revista de acceso abierto). En este trabajo se estudia el comportamiento de la mosca de la fruta -uno de los sujetos favoritos de experimentación por parte de los biólogos- y se intenta modelar el mismo. La idea básica que podemos tener sobre estos insectos es que son seres fundamentalmente reactivos: su comportamiento se describiría mediante una asociación entre estímulos y acciones. Sin embargo, una ligera inspección revela que éste no es el caso, ya que no siempre se responde al mismo estímulo con la misma acción. La solución inmediata es suponer que hay algún efecto aleatorio, algún tipo de ruido blanco que afecta a la toma de deciciones, tal como se ilustra en la figura inferior.

Source: A. Maye et al., PLoS ONE 2(5): e443, 2007

¿Es este modelo realista? Eso es lo que se ha pretendido analizar en este trabajo. Para ello se ha considerado un enfoque experimental en el que se aísla a las moscas de estímulos externos (una especie de tanque de privación sensorial), y se analiza su trayectoria de vuelo. De manera más precisa, se examina la distribución temporal de los cambios de dirección. Dado que los estímulos externos están controlados, esta distribución proporciona información muy valiosa sobre los mecanismos que controlan la toma de decisiones.

Los resultados del análisis son sumamente interesantes. En primer lugar, se descarta que el mecanismo subyacente en el cerebro de la mosca sea una función determinista afectada por ruido blanco: la desviación de la distribución de intervalos entre cambios de dirección con respecto a una simulación de una distribución de Poisson es significativa. La distribución real exhibe además algunas propiedades llamativas tales como una cola larga, una de las características distintivas de las leyes de potencias:

Concretamente, podría tratarse de una distribución de Lévy, que exhibe un régimen de ley de potencias en el extremo de la distribución. Este tipo de distribuciones suele surgir de la interacción entre varios subsistemas no-lineares. Lo más común es que se trate de procesos estocásticos sin memoria en los que cada valor de la secuencia temporal depende únicamente del anterior. Esta explicación sigue sin ser del todo satisfactoria sin embargo. Si se supone que las secuencias son el resultado de un sistema no-linear con dinámica caótica, y se calcula la dimensión fractal del atractor, se encuentran diferencias significativas entre los modelos puramente aleatorios, y los datos experimentales.

La conclusión de los autores es que en el cerebro de las moscas hay lo que denominan un iniciador, un proceso determinista altamente no-lineal y muy complejo. Dada la sensibilidad a las condiciones iniciales (característica básica de los sistemas caóticos), este iniciador sería el responsable del comportamiento aparentemente espontáneo de la mosca. Se tiene constancia por otra parte de que este tipo de comportamiento es evolutivamente favorable, tanto desde el punto de vista de la exploración en busca de alimento, como por la presión selectiva que introduce durante el proceso de apareamiento.

Source: A. Maye et al., PLoS ONE 2(5): e443, 2007

Es sorprendente la extraordinaria complejidad subyacente al comportamiento aparentemente simple de una mosca. En relación al debate anterior sobre mente y calculabilidad, esta complejidad no supone en principio que exista ningún proceso no computable. Sí es interesante considerar que el hecho de que exista este extraordinario nivel de complejidad en este tipo de organismos pone de alguna manera el listón muy alto para lo que podemos encontrarnos más arriba en la cadena evolutiva. Por otra parte, la presencia de este tipo de iniciadores con extrema sensibilidad a las condiciones iniciales puede conducir a pensar (o al menos a no descartar) que incluso pequeñas desviaciones debidas a fenómenos cuánticos afecten de manera significativa al comportamiento emergente del organismo.

Turing en una cáscara de nuez: castores afanosos y la paradoja de Berry

Siguiendo la serie sobre computabilidad, hoy nos vamos a fijar en una función muy interesante, y que nos va a servir de nexo entre computación e información. Se trata de la función castor afanoso (busy beaver en inglés), y que podemos definir informalmente como el mayor valor que un algoritmo de cierto tamaño puede producir. De manera más precisa, supongamos un cierto formalismo para describir algoritmos, y consideremos una función que cuantifique el tamaño de una cierta descripción. Por ejemplo, podemos considerar máquinas de Turing con un alfabeto binario, y usar el número de estados como indicación del tamaño, o un cierto lenguaje de programación de alto nivel, y emplear como medida de tamaño de un programa su número de símbolos o de instrucciones (la elección que hagamos afecta a los valores particulares de la función, pero no a su esencia). Una vez tenemos esto, si A es un cierto algoritmo (que computa una función definida para el valor de entrada 0), emplearemos |A| para indicar su tamaño. Ahora, definimos la función Σ(n) como

esto es, el mayor valor computable por un algoritmo cuya descripción tiene una cierta complejidad (también se puede considerar alternativamente S(n), el mayor número de pasos que realiza un algoritmo de tamaño n antes de detenerse). Consideremos en primer lugar que se trata de una función que crece muy rápidamente. Por ejemplo, cuando hablamos de números grandes dimos una descripción muy concisa del número de Graham (una cantidad cuyo tamaño es simple y llanamente aberrante). Es posible entonces construir un algoritmo relativamente simple que lo calcula (no habría evidentemente forma de almacenarlo ni en un trillón de universos, pero ésa no es la cuestión), lo que evidencia que incluso para valores pequeños del parámetro de entrada, la función Σ(n) devuelve valores astronómicos. Consideremos por otra parte que se trata de una función bien definida: para cada tamaño n, hay un cierto algoritmo que calcula el valor más grande (o varios empatados, que para el caso es lo mismo). Por supuesto, dado un tamaño n hay programas que no se detienen, y que no nos interesan. Dado que el problema de la parada no es computable, por aquí podemos a empezar a ver la dificultad que plantea esta función. De hecho, la función Σ(n) no es computable.

Antes de ver una demostración formal de porqué no es computable esta función, resulta interesante considerar la paradoja de Berry. Esta paradoja se puede plantear de diferentes formas, pero consideremos la siguiente:

Uno más que el mayor número expresable con menos de veinte palabras.

Es fácil ver que esta expresión tiene menos de veinte palabras, y que supuestamente representa un número x. Sin embargo, de ser así, este número x sería estrictamente mayor que el máximo valor del conjunto de todos los números expresables con menos de veinte palabras, conjunto al que el propio x pertenece, lo que resulta en una contradicción. Esta paradoja es en el fondo el motivo por el que la función castor afanoso no es computable. De manera más precisa, supongamos que Σ(n) es computable. Podemos entonces definir una función M como sigue:

Sea |M|=w. Definamos ahora F_w(n) como

Podemos asumir que |F_w|=2w (por ejemplo, sumar w puede hacerse mediante w instrucciones de incremento). Por la propia definición de la función Σ(n) tenemos que cuando n=2w

Llegamos a una contradicción, lo que invalida nuestra suposición inicial de que Σ(n) era computable. La demostración de incalculabilidad de S(n) es más simple todavía, ya que si sabemos el número máximo de pasos que da una máquina de complejidad n antes de detenerse, podemos determinar si una máquina arbitraria se para o no, simplemente simulándola durante dicho número de pasos: si no se para al llegar a ese límite, ya sabríamos que no se pararía nunca.

Tal como apuntaba al principio, uno de los aspectos más relevantes de esta función es como relaciona la complejidad de la descripción de un programa con lo que éste puede calcular. El próximo día habrá ocasión de profundizar en esta relación, que ofrece algunos resultados sumamente interesantes.

    

Turing en una cáscara de nuez: Teorema de Rice (o por qué ningún antivirus será fiable al 100%)

En el último artículo sobre Turing vimos como hay ciertos problemas cuya resolución no es abordable mediante un proceso algorítmico. Esto lo ejemplificamos a través del problema de la parada, pero hay muchos otros problemas que resultan ser no computables. Por ejemplo, también vimos como el reconocimiento de resolutores parciales de parada (i.e., determinar si un programa arbitrario da siempre o bien soluciones correctas al problema de la parada, o bien no da solución) era un problema no computable: si fuera computable, podríamos construir una solución algorítmica al problema de la parada, cosa que sabemos que es imposible. Esta estrategia de reducir el problema de la parada (o en general, cualquier otro problema que se sepa no-computable) a un cierto problema P es la más común para determinar la no-computabilidad del mismo. Por ejemplo, consideremos el problema de la equivalencia: dados dos programas determinar si son equivalentes, esto es, si computan la misma función. Intuitivamente, podemos ver que dar respuesta a este problema implica ser capaz de determinar si las salidas de dos programas arbitrarios son iguales para cierta entrada, lo que significa ser capaz de determinar si se detienen o no para la misma. De manera más genérica, podemos recurrir a un resultado sumamente poderoso en este campo: el Teorema de Rice. Básicamente, el Teorema de Rice nos dice:

Dada una propiedad no trivial de las funciones parciales, no es computable determinar si una función arbitraria la posee o no.

En la anterior definición, una propiedad es no trivial si hay funciones que la tienen, y otras que no. La demostración del teorema se basa precisamente en explotar la posibilidad de resolver el problema de la parada si tuviéramos un reconocedor de propiedades no triviales. Así, supongamos que tenemos una cierta propiedad A no trivial. Eso quiere decir que hay al menos una función F_sí que la tiene, y una función F_no que no la tiene. Supongamos ahora que tenemos un algoritmo R_A definido como

Definamos ahora un programa T_m,n(i) que primero calcula F_n(m) y luego calcula F_sí(i), valor este último que se devuelve como resultado. Puede verse que este programa devuelve lo mismo que F_sí(i), y por lo tanto tiene la propiedad A, sí y sólo si F_n(m) se para. Si w(m,n) es la codificación del programa T_m,n, entonces podemos definir un algoritmo para determinar la parada como H(m,n) = R_A(w(m,n)). Como esto es imposible, se sigue que no existe R_A (si la propiedad A fuera algo que F_n(m) cumple al no pararse, hubiéramos podido hacer un razonamiento similar empleando F_no en lugar de F_sí).

Las aplicaciones del Teorema de Rice son enormes. Por ejemplo, no es computable saber si una función arbitraria se detiene para algún valor de entrada (hay al menos una que sí lo hace, y otra que no, por lo que se trata de una propiedad no trivial). Otro ejemplo más práctico: no es computable determinar si un programa es un virus/troyano/… que realizará acciones maliciosas (definidas de alguna manera conveniente, como por ejemplo, escribir en cierta zona reservada de memoria, copiarse a sí mismo en otro programa, etc.). Esto no quiere decir que ningún virus/troyano/… sea detectable, sino que para cualquier procedimiento de detección fiable, siempre se puede definir un programa malicioso que lo burle. Esto tiene dos consecuencias prácticas fundamentales: (1) no hay protección fiable al 100%, y (2) la falta de seguridad hay que compensarla con falsos positivos.

Si alguien no termina de estar del todo convencido de que la detección de programas maliciosos no es computable, he aquí una demostración directa a través del corte diagonal. Sea M(m,n) un supuesto algoritmo no malicioso que determina si F_n(m) ejecuta código malicioso. Sea V(m) un programa que siempre ejecuta código malicioso para cualquier valor de m. Definamos el algoritmo S(m) como

El anterior algoritmo tendrá una codificación s. ¿Es malicioso S(s)? Si lo es, entonces M(s,s)=1, por lo que S(s) simplemente devuelve 0, sin hacer nada más, luego no es malicioso (salvo que la comprobación M(s,s) lo fuera, lo que suponíamos falso de partida). Si no lo es, entonces M(s,s)=0, por lo que se ejecuta el código malicioso, lo que es otra contradicción. Conclusión, el supuesto algoritmo M no existe. Esta demostración es en principio más débil que la del Teorema de Rice, ya que deja abierta la posibilidad a detectores maliciosos, pero podemos soslayar esta limitación haciendo que la ejecución de M se haga enteramente sobre una sistema de memoria diferente del que empleamos para S (sería una emulación perfecta de M sobre un computador virtual que se crearía para la ocasión, y que se destruiría luego).

Turing en una cáscara de nuez: No computabilidad

Cuando empezamos a hacer el recorrido por los resultados de Gödel ya teníamos en perspectiva cómo eventualmente llegaríamos a enlazarlos con la noción de no-computabilidad. De hecho, esta noción emana de manera natural de los teoremas de incompletitud, y viceversa: partiendo de la noción de no-computabilidad llegamos a la conclusión de que la consistencia y la completitud de un sistema formal lo suficientemente complejo son características incompatibles entre sí. Vamos a ver por qué sucede esto, y para ello es necesario partir de una definición de computabilidad que nos permita entender qué quiere decir no-computable.

Intuitivamente y sin entrar en muchos detalles, la noción de computabilidad en relación a un cierto problema hace referencia a la posibilidad de disponer de un algoritmo para resolverlo, esto es, que exista un procedimiento mecánico, con descripción finita y no ambigua, y que resuelva dicho problema en tiempo finito. Esto enlaza claramente con el programa formalista de Hilbert, en el que se pretendía tener un procedimiento de este tipo para demostrar/refutar cualquier afirmación matemática expresada en ese hipotético sistema formal definitivo que se anhelaba. En este contexto, el que Gödel hubiera demostrado en su denominado Teorema de Completitud que toda afirmación universalmente válida en la lógica de primer orden es demostrable, conducía a la cuestión obvia de encontrar esa demostración (o determinar su inexistencia) para una cierta expresión lógica. Si nos fijamos un poco, es fácil ver que esta cuestión en el fondo se reduce a determinar si existe una demostración o no, ya que una vez se ha determinado que existe, basta generar sistemáticamente todas las demostraciones (por ejemplo, ordenadas crecientemente por su número de Gödel) hasta dar con la demostración que nos interesa. La determinación de la existencia de una demostración para una fórmula arbitraria de la lógica de primer orden es lo que se conoce como problema de la decisión (Entscheidungsproblem en alemán).

¿Existe algún procedimiento mecánico (un algoritmo) para resolver el problema de la decisión? La respuesta es «no». Para ver por qué partamos de algún tipo de formalismo para expresar algoritmos, por ejemplo una máquina de Turing (MT). Los detalles del formalismo son realmente poco importantes aquí, pero sí es interesante el hecho de que una MT captura bien la idea intuitiva de procedimiento secuencial, en el que se van realizando acciones paso a paso, y se van tomando decisiones sobre qué acciones realizar. En el marco de un procedimiento de este tipo es natural preguntarse sobre si acaba eventualmente o no. Para formalizar un poco esta idea, consideremos en primer lugar que una MT es una descripción finita de un procedimiento, por lo que podemos codificar dicha descripción como un número natural, de manera similar al proceso de gödelización. Así, M_n es la MT cuya codificación es el número n. Del mismo modo, si el procedimiento admite unos datos de entrada, éstos serán también finitos y representables mediante otro número natural. Diremos entonces que M_n(m) -donde m,n son números naturales- es el resultado de aplicar M_n a los datos de entrada representados por m. En caso de que M_n(m) no se detuviera, diremos que M_n(m)=■.

Vamos a plantearnos ahora la cuestión de si una MT particular se para con unos ciertos datos de entrada o no. Supongamos que se trata de una cuestión computable, esto es, que existe una MT H que tomando como entradas m y n determina si M_n(m) se para o no. Por ejemplo,

Es fácil demostrar que esta MT no existe haciendo uso del corte diagonal. Para ello, definamos F(n) = 1 + H(n,n) · M_n(n), es decir,

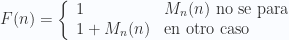
Si H existe, no hay dificultad en definir una MT como F, cuya codificación será un cierto valor r (es decir, M_r=F). Ahora, ¿se detiene F(r)?

• Si la respuesta es afirmativa, entonces H(r,r) = 1, con lo que F(r) = 1+F(r), lo que es una contradicción.
• Si la respuesta es negativa, entonces H(r,r) = 0, con lo que F(r) = 1, lo que no tiene sentido, ya que F(r)=■.

Llegamos a una contradicción en ambos casos, por lo que la suposición de partida -que existe H– es falsa. La única posibilidad que tendríamos de escapar de la contradicción es pensar que H es sólo un resolutor parcial de parada (PHS, por sus siglas en inglés), es decir, que puede determinar correctamente si algunos procedimientos se paran o no, pero a veces el propio H no llega a pararse. En otras palabras, H daría una respuesta correcta, o no daría respuesta. En ese caso, no hay inconveniente en suponer que F(r) no se para (i.e., H(r,r) = ■, F(r) = ■). El problema es que no tenemos forma de determinar en general si H es un PHS fiable. Si lo pudiéramos determinar, esto es, si existiera un procedimiento R tal que

entonces podríamos definir un procedimiento X_N

donde N es una cierta constante. La codificación de X_N sería w, o más precisamente w(N), dependiendo del valor de N. Definamos ahora un procedimiento Q(n)=R(w(n)). Este procedimiento devolverá 1 si, y sólo si, X_n está en lo cierto al decir que M_n se para (asumimos sin pérdida de generalidad procedimientos sin datos de entrada), es decir, tendríamos un resolutor completo de parada. Como esto es imposible, no podemos disponer por lo tanto de un reconocedor de resolutores parciales de parada.

Hemos encontrado un problema al que no podemos dar respuesta computacionalmente. Las implicaciones de este hecho son enormes. Podemos por ejemplo desandar un poco el camino, y ver que la cuestión de la detención de una cierta MT es expresable mediante una fórmula lógica de primer orden. El que se trate de un problema no computable implica que dicha fórmula es indemostrable e irrefutable, lo que nos lleva a dar una respuesta negativa al problema de la decisión, y enlazar con el primer Teorema de Incompletitud de Gödel. Con todo y con ello, lo más interesante es la cantidad de problemas aparentemente simples que por mor de la no-computabilidad del problema de la parada resultan ser no-computables también. Otro día veremos algunos de ellos.

Gödel en una cáscara de nuez: Segundo Teorema de Incompletitud, y Teorema de Completitud

Cuando empezamos a recorrer los resultados de Gödel y mencionamos el contexto histórico mereció especial atención el programa formalista de Hilbert. Hay que recordar que el objetivo de Hilbert era definir un sistema formal completo y consistente, dentro del cual poder razonar de manera mecánica sobre cualquier noción matemática. El primer teorema de incompletitud que vimos hace unos días asestó un golpe letal a esta pretensión: en cualquier sistema formal consistente lo suficientemente complejo como para englobar a la aritmética de Peano hay afirmaciones lógicas que son indemostrables e irrefutables. Dando por perdida pues la completitud, nos podemos aferrar a la consistencia: si somos capaces de probar que nuestro sistema es consistente, tendremos al menos una garantía de la solidez de las demostraciones que hagamos dentro de él. Aquí es donde entra el segundo teorema de incompletitud para rematar definitivamente las aspiraciones de Hilbert.

El segundo teorema de incompletitud de Gödel surge casi como un corolario del primero, aunque su trascendencia es sin embargo muy grande. Recordemos que el primer teorema de incompletitud afirmaba que había una fórmula G (realmente la fórmula G depende del sistema S, por lo que deberíamos emplear la notación G_S, pero mantendremos la G por simplificar), tal que ni G ni ~G eran demostrables dentro del sistema si éste era consistente. Siguiendo con la notación que empleamos:

Recordemos también que G se define como:

por lo que es fácil ver que si tenemos una demostración de la consistencia del sistema, tenemos también una demostración de la indemostrabilidad de G, y por la propia definición de G esto significa que hemos demostrado G. Dado que sabemos que tal demostración nos lleva a la inconsistencia, hemos de concluir que nuestra suposición de partida -la existencia de una demostración de consistencia- es falsa. No podemos por lo tanto demostrar la consistencia del sistema dentro del mismo.

Aunque en su momento los teoremas de incompletitud supusieron un gran impacto, y de hecho acabaron con las ambiciones formalistas de Hilbert, vistos con retrospectiva son la consecuencia evidente de la metodología que se pretendía seguir, basada en la manipulación mecánica de símbolos y fórmulas mediante unos ciertos procedimientos bien definidos. Esto se puede apreciar más claramente si nos fijamos en un resultado anterior del propio Gödel que -quizás para complicar la cosa- se ha venido a denominar el teorema de completitud de Gödel. Este teorema captura muy bien la pretensión de Hilbert, y explica por qué ésta no es posible (o al menos se puede extraer una interpretación a posteriori del porqué).

La clave del teorema de completitud de Gödel es la idea de modelo. Básicamente, cuando definimos el sistema formal especificamos una sintaxis para expresar las fórmulas, así como unos ciertos axiomas y reglas de inferencia. Lo que tenemos ahí es una mera descripción sintáctica, que una vez dotada de una interpretación semántica, da lugar a un modelo del sistema. Por ejemplo, podemos considerar un sistema definido sobre la base de un conjunto de objetos X, y una operación interna binaria que es asociativa, conmutativa, tiene elemento neutro, y cada elemento de X tiene un inverso. Como puede apreciarse, lo que estamos definiendo aquí es un grupo abeliano. Podemos ahora dar una interpretación del conjunto X y de la operación binaria, por ejemplo, los números enteros y la suma, o los reales (menos el 0) y la multiplicación. Si demostramos algo sin hacer uso de una interpretación concreta, entonces eso debera ser cierto para todas las interpretaciones (o modelos) posibles. Decimos entonces que ese algo es universalmente válido para ese sistema.

El teorema de completitud de Gödel afirma que toda fórmula universalmente válida es demostrable. Esto puede comprobarse como sigue: supongamos que tenemos un sistema S y que hay una fórmula F que es universalmente válida para él pero que no es demostrable en él. Podemos construir ahora un sistema S’ en el que incluimos ~F como axioma, lo cual no nos ocasiona contradicción sintáctica ya que F no es demostrable. Según el teorema de existencia de modelos de Henkin, si un sistema es consistente, entonces tiene un modelo M. En dicho modelo será cierto ~F (que es un axioma) y F (que era universalmente válido en S, del que M es también modelo). Llegamos a una contradicción, luego F ha de ser demostrable.

A la luz de lo anterior, puede verse claramente que si algo es universalmente válido debe ser demostrable, y por lo tanto si algo no es demostrable es porque no es universalmente válido. No debe entonces sorprendernos que un sistema consistente sea incompleto: hay formulas que serán ciertas en unos modelos y falsas en otros, por lo que no podemos esperar demostrarlas o refutarlas abstrayéndonos de su interpretación. Esto que puede parecer evidente ahora, no lo era tanto en la época de Gödel (el trabajo de Henkin es de hecho muy posterior al de Gödel).

La noción de validez universal es el eslabón que nos va a permitir enlazar el trabajo de Gödel con la idea de computabilidad. No es la única conexión, pero sí es el enlace histórico que nos lleva por ejemplo al trabajo de Turing. Ésa será la próxima parada.

    

Gödel en una cáscara de nuez: Primer Teorema de Incompletitud

Tras haber visto anteriormente el corte diagonal de Cantor, podemos hacer ya una incursión en el terreno de los teoremas de incompletitud de Gödel. Para ello, hay que empezar por enmarcar el contexto en el que estos teoremas se formulan, tanto desde el punto de vista histórico, como desde el punto de vista formal. Con respecto a lo primero, hay que hacer mención sin duda a la enorme figura de David Hilbert, y en particular a su programa formalista. De acuerdo con la visión de Hilbert, todas las ramas de las matemáticas se podrían llegar formalizar en un sistema completo (en el que todo lo que fuera cierto fuera demostrable), consistente (en el que no se pudieran demostrar cosas falsas), y decidible (la verdad o falsedad de una afirmación matemática sería demostrable mediante un procedimiento mecánico bien definido). Esta última parte -la decibilidad- hace evidentemente referencia a la noción de algoritmo, que no obstante no estaba aún formalizada tal como la entendemos actualmente. Éste será precisamente el vínculo que nos permitirá enlazar los resultados de Gödel con los de Turing más adelante.

Fue en pleno apogeo del programa de Hilbert en el que Gödel presentó los teoremas de incompletitud que dieron al traste con el mismo. El marco formal en el que dichos teoremas se encuadran es el de la lógica de primer orden. En dicho marco empleamos predicados para razonar acerca de un conjunto de objetos. Mediante estos predicados podemos realizar afirmaciones sobre objetos concretos (por ejemplo, par(2), que podríamos interpretar como «2 es par»), o expresar afirmaciones más genéricas mediante el uso de variables y cuantificadores. Por ejemplo:

Por supuesto, debemos disponer también de unos axiomas, que establezcan verdades básicas de partida, y un conjunto de reglas de inferencia que nos permitan demostrar la verdad o falsedad de una afirmación como la anterior. De hecho, si la ambición de Hilbert fuera factible, dada una afirmación cualquiera (y no sólo en el marco de la lógica de primer orden) se podrían aplicar de forma mecánica las reglas de inferencia hasta o bien demostrar dicha afirmación (en cuyo caso sería cierta) o su negación (en cuyo caso sería falsa). Gödel demostró que esto no es posible, ya que un sistema lo suficientemente complejo como para permitir expresar y demostrar verdades aritméticas sobre los números naturales (esto es, un superconjunto de la aritmética de Peano), será o bien inconsistente (en cuyo caso se podrá demostrar cualquier cosa), o incompleto (en cuyo caso habrá afirmaciones indemostrables e irrefutables).

La base de los teoremas de incompletitud es lo que se conoce como aritmetización, numeración de Gödel, o simplemente gödelización. Gödel definió un procedimiento que permite codificar una secuencia de símbolos en un número natural. Los detalles de como conseguir esto no son importantes en este momento, pero a grandes rasgos se basan en el hecho de que la descomposición en factores primos de un número es única. De esta forma, se puede asociar a cualquier fórmula lógica (o secuencia de fórmulas lógicas) F un número natural g(F). Esta posibilidad resulta crucial aquí, ya que es la que nos va a permitir expresar la auto-referencia y en última instancia aplicar el corte diagonal.

Una vez tenemos formulas y demostraciones codificadas mediante números naturales, es fácil expresar la noción de demostrabilidad mediante una fórmula lógica D(x,y), que interpretaremos como «x es el número de Gödel de una demostración de la fórmula cuyo número de Gödel es y«. Por lo tanto, una fórmula F será demostrable (cosa que indicaremos por P(x), donde x=g(F)) si tiene al menos una demostración, esto es:

Ya estamos listos para aplicar el corte diagonal. Definamos para ello la noción de auto-indemostrabilidad Q(x) como

,

es decir, una formula F es auto-indemostrable si no se puede demostrar F(g(F)). ¿Qué ocurre cuando F=Q, esto es, es demostrable que no hay demostración para G=Q(g(Q))? Analicemos las posibilidades:

• Supongamos que sí es demostrable, esto es, que P(g(G)) es cierto, y por lo tanto existe un y tal que D(y,g(G)) es cierto. En este caso, nótese que D(y,g(G)) = D(y,g(Q(g(Q)))). Sin embargo, que Q(g(Q)) sea cierto implica por su propia definición que no existe ningún y para el que D(y,g(Q(g(Q)))) sea cierto. Luego habríamos demostrado algo falso, y el sistema sería inconsistente.
• Supongamos que no es demostrable. Volvamos entonces nuestra atención hacía su negación. Si existe un y tal que D(y,g(~G)) es cierto quiere decir que ~Q(g(Q)) es cierto, esto es, que existe un z tal que D(z,g(Q(g(Q)))) = D(z,g(G)) es cierto. Esto contradice nuestra suposición de partida de que G era indemostrable, y en cualquier caso produce una inconsistencia al haber una demostración de G y de ~G.

El razonamiento anterior puede ser algo farragoso, pero en esencia se reduce al hecho de que G afirma su propia indemostrabilidad. Si G es demostrable, entonces es falso y al haber demostrado algo falso nuestro sistema es inconsistente. Si su negación es demostrable, entonces por definición G es demostrable, con lo que el sistema es nuevamente inconsistente (ya que hemos demostrado algo y su negación). Por lo tanto, si el sistema es consistente, ni G ni ~G son demostrables, luego el sistema es incompleto.

Es importante notar el hecho de que en ningún momento se afirma que G sea cierta o no, sólo que ella y su negación son indemostrables si el sistema es consistente. Sin embargo, si analizamos la situación podemos llegar a la conclusión de que sí es cierta: desde nuestro punto de vista externo al sistema, está claro que no hay demostración de G, que es lo que G afirma, por lo que debe ser cierta. Que podamos percibir este hecho es uno de los argumentos más frecuentemente invocados para sostener que nuestra mente no es algorítmica, y por lo tanto negar la posibilidad de que pueda ser representada mediante un modelo computacional equivalente a una máquina de Turing. Esto merece comentario aparte en un futuro artículo.